Articles & Posts
- Printing Photos from the Linux Command Line Here’s a handy script that lets you leave your printer in its default mode (i.e. configured for printing ordinary documents on letter or A4) but also print photos from the command line. The handy thing here is you can then skip the annoyance of manually editing a bunch of printing menus to configure the paper size, tray, glossy paper, DPI, 4x6” page size, and a specific color profile.
- Backing up Postgres Databases with Docker Docker is a pretty good abstraction, but has it some leaks. Today I was trying to deploy a test Postgres database with some data stored in it, and ran into problems shipping the data around between my machines using Docker.
- Symmetric Encryption in Python Hashing strings is useful for creating unique identifiers for strings, blobs of data, etc. In Python, it’s sometimes handy to make your own hashing function from AES. Here’s a brief snippet of how to do that for short messages. Kind of fun!
- Nodemon HTTP Server While playing with three.js today, I needed a hot-reloading JS webserver in a real hurry to serve out content. Here’s how to start a server at http://localhost:8080/ in just three lines:
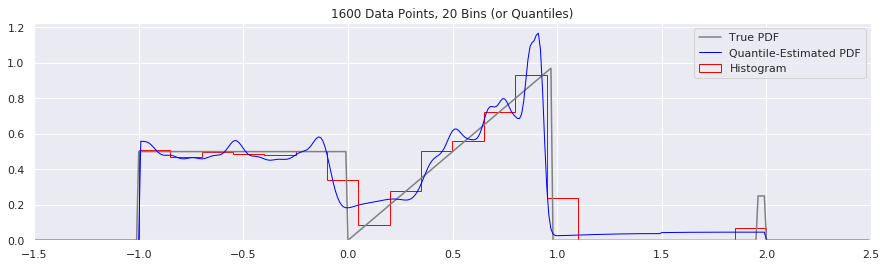
- Preferring Quantiles to Histograms The histogram is most scientists’ tool of choice for viewing the distribution of values of a single variable. But lately I have been exploring an alternative: quantiles (e.g. deciles, percentiles, etc). Although viewing data in this way is not perfect, it has several advantages to histograms, including robustness to outliers and a freedom from apriori assumptions about the range or smoothing level of the data.
- Jupyter Quick Install for Scientists Python is a good language, but its tooling (like pip, conda, setup.py, setup.cfg, requirements.txt, and the awkward support for binaries needed for libraries like scipy, keras, etc), leaves much to be desired. And for most scientists, it’s simply not interesting using all these build tools when you just want to get coding quickly on a new machine.
- Automatic CSV to SQL ETL in Clojure This is another basic example to help beginners get started in Clojure, which is still my favorite programming language, almost 10 years after I first started using it. Like all languages, Clojure has some warts. But it also has a lot of very powerful and abstract concepts that many average programmers have not seen before, and like most mathematical concepts, the power of such abstractions are greatly underestimated by many people. Even fancy-sounding but easy-to-understand concepts like homoiconicity are still really underappreciated in the programming community.
- Notes on CSS Popup Tooltips Front-end website development is not my strongest area, so I’m just going to share some notes I took on how to make a hover “tooltip” on some text using CSS. I have a feeling this will come up again as handy sometime.
- Python CSV Load Times and the Feather Format One of the most common data science tasks is loading structured data in tabular form. For “small data”, a popular format is often Comma-Separated-Value (CSV), which nearly everybody can read and write correctly. For so-called “big data”, one often needs a database, preferably SQL database like Postgres, or if the dataset gets very large, then often NoSQL becomes the only practical choice. Well, what do you do when you have “medium data”? Data that is still small enough to fit on a single computer, but is too large to load into memory?
- Composite Robot Construction This article describes the progress of a fiber-reinforced polymer monopod robot that I built over a period of about 30 days. My hope is that seeing some of the successes and failures I encountered will help you build your own composite robots. Foam and fiberglass are very versatile materials that are just as accessible to garage-level workshops as they are to research institutions, as I hope you will see.

- Loading CSVs in Clojure Loading CSVs in Clojure is really easy using clojure.data.csv. Depending on what you will do with the data, you can either represent it in tabular form (as a vector of vectors), or as a list of hashmaps. Both approaches have their advantages and disadvantages, and here are some very stock functions for how to achieve that:
- A Localhost Swagger Editor I’ve always edited swagger docs using the online editor, but thanks to docker, you may run it locally with equal ease:
- A Metta Meditation Sometimes, the best thing to do when you hear a good idea is just to pass it on.
- Connecting a Clojure REPL to a PostgreSQL Docker Container In this tutorial, we’ll launch Postgres (a.k.a. PostgreSQL) in a Docker container, create a Postgres database, and connect to it from a Clojure REPL. Postgres is a great open source SQL database with a long history, and is a good choice for many small-to-medium scale projects.
- Packaging and Running Clojure Apps Locally with Docker This is just a simple tutorial on how to package and deploy a Clojure application to a Docker file, which can then be deployed locally, on a server, or in the cloud.
- Adding Page Numbers to PDFs This is just a post to share a simple bash script for automatically adding page numbers to PDF files. It’s particularly handy when you need to renumber a new document that is the concatenation of multiple scanned PDFs that were concatenated using pdfunite, a useful command line tool on Debian.
- Layered Tetrahedral Geometric Structures This article describes another iteration of the dome-like structure that I discussed a few months ago. I still don’t have a good vocabulary for describing why I think these things are neat, except to say that I somehow find it relaxing to work on toy engineering problems once or twice a month. I guess de gustibus non est disputandum – “there’s no accounting for (bad) taste!”

- The Reinforced Pentakis Dodecahedron Dome For your amusement, I would like to present a reinforced version of a geodesic dome that is many times stronger than conventional geodesic domes. It is essentially two concentric domes, one nested inside the other, connected entirely by tetrahedra in a way that both strengthens the dome and provides space for insulation. Compared to single-layer geodesic structures, this new structure uses about 2-3x more materials, but it is so much stronger that it is startling.

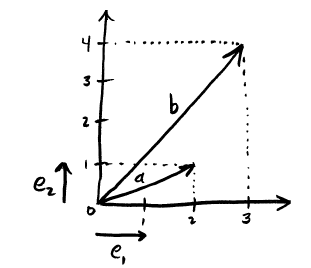
- Introduction to Geometric Algebra, Part 1 Geometric Algebra (GA) is one of those things that we should have all learned in high school because it would have made physics and mathematics in college so much easier.
- Hyperbolic Geometry & Special Relativity While studying An Introduction to Particle Physics on a recent flight to Japan – studying math that is way above my head is a nerdy hobby of mine – I came across a simple viewpoint on special relativity that really stunned me:
- Reviving the Dead...Content From 2003 until 2016, I had a personal website at roboloco.net. It lasted until last year, when I finally grew tired of upgrading applications, keeping comments free of spam, and the servers secure from hackers and the occasional website defacement. Thank you, GitHub, for providing this terrible sysadmin a free place to store this content, and one that requires no regular maintanance!
- Project Euler Problem 89 Problem 89 was kind of fun: we needed to convert some sloppily written roman-numerals into their more efficient, minimal representations.
- Project Euler Problem 87 Problem 87 asks us to find how many numbers below 50 million that can be expressed as the sum of a prime square, cube, and fourth power.
- Project Euler Problem 86 Despite it’s relative simplicity, I wasted hours on problem 86. One important thing that I learned is:
- Project Euler Problem 85 Problem 85 asks us to find the number of rectangles that can be drawn in a grid of size m by n.
- Project Euler Problem 84 Problem 84 asks us to implement the classic game Monopoly and find the most-visited spaces on the board…if we used two 4-sided dice instead of 6-sided ones.
- Project Euler Problem 83 Problem 83 can be solved with A* exactly like the we did in problem 81. The only code that needs to be changed is the neighbors function neigh and the estimated cost-to-goal function est. Everything else can be reused from problem 81.(defn euler-83 [] (let [mat (load-matrix "/zzz/work/matrix.txt") m (count mat) n (count (first mat)) cost (fn [[i j]] (nth (nth mat (dec i)) (dec j))) start [1 1] goal [m n] goal? (fn [e] (= e goal)) est (fn [[i j]] 0) neigh (fn [[i j]] (merge (when (< i m) {[(inc i) j] (cost [(inc i) j])}) (when (< j n) {[i (inc j)] (cost [i (inc j)])}) (when (< 1 i) {[(dec i) j] (cost [(dec i) j])}) (when (< 1 j) {[i (dec j)] (cost [i (dec j)])}))) path (a*-search est neigh start goal?)] (reduce + (map cost path))))
- Project Euler Problem 82 As I mentioned in the previous post (#81), we can use [A](http://en.wikipedia.org/wiki/A) to easily solve problem 82 as well.
- Project Euler Problem 81 I’m actually a little proud of this one – this simple implementation of A* search seems to be one of the prettier pieces of code I have written, and it was implemented abstractly enough to solve problems 81, 82, and 83 without changing the core algorithm.
- Project Euler Problem 80 It took us until the 80th problem to find one, but we finally found an ugly wart in Clojure 1.2: big square roots. At the time of writing, it does not properly accommodate bigdec numbers. Look at this ugly behavior:(expt 12 34) ;; 4922235242952026704037113243122008064 ... a bignum.(expt 12 (/ 34)) ;; 1.0758225047262997 ... a double!(with-precision 100 (expt 12 (/ 34))) ;; 1.0758225047262997... still a double!
- Project Euler Problem 79 Problem 79 asks us to crack a primitive security ‘feature’ asked by some (hypothetical) banks. Given 50 successful login attempts using an ordered subset of the digits from a passcode, we need to find what the original passcode was.
- Project Euler Problem 78 Problem 78 is the third and final of the integer partitioning problems, but because of the rather large number of possibilities it was rather more difficult.
- Project Euler Problem 77 Problem 77 tests our ability to write correct, reusable code because problems 76, 77, and 78 all use roughly the same algorithm and ask for integer partitions of a particular number. This time, the partitioning must be done using only prime numbers.
- Project Euler Problem 76 Often the hardest part about Project Euler is to discover what page of wikipedia to read for the mathematical theory behind the problem. In the case of problem 76, we need to do some reading on Integer Partitions.;; A renamed function from Problem 31(defn integer-sums [c v] (let [f (first c)] (if (= f 1) 1 (reduce + (for [n (range 0 (inc (quot v f)))] (integer-sums (rest c) (- v (* n f))))))))
- Project Euler Problem 75 Once again, to solve Problem 75 our first stop should be Wikipedia’s page on Pythagorean Triples.
- Project Euler Problem 74 Problem 74 concentrates yet again on factorials, sums of digits, and chains of computation. To be honest, I am pretty sick of this type of problem, so here is my inelegant brute force solution.(def factorial-char (zipmap "0123456789" (conj (reductions * (iterate inc 1)) 1)))
- Project Euler Problem 73 Project Euler Problem 73 continues the sequence of problems related to Farey Sequences. This time, we are asked to find the number of proper fractions between 1/3 and 1/2 with denominators less than 12,000.
- Project Euler Problem 72 My solution to Project Euler Problem 72 is rather simple. We are asked to find the length of a Farey Sequence for all fractions with denominators less than one million.
- Project Euler Problem 71 Problem 71 asks us to find a proper fraction just slightly less than 3/7, with a denominator less than one million.
- Project Euler Problem 70 Problem 70 was another problem that is nearly impossible to accomplish without spending time to understanding the math. A brute force approach will be far to computationally expensive to work, although it took me a few tries to discover this.
- Project Euler Problem 69 After a long and wonderful three week vacation (and another week of just getting back into the flow), it’s time to return to the daily little bit of practice to stay sharp. Let’s get started!
- Project Euler Problem 68 Problem 68 was one of those strange problems where you start with 23 lines of code that take 77 seconds to run, and by the time you are done thinking about the problem, you end up with 6 lines of code that takes 0.1 milliseconds to complete.
- Project Euler Problem 67 Problem 67 is just a harder version of problem 18.
- Project Euler Problem 66 Problem 66 asks us to find integer solutions of a quadratic Diophantine equation.
- Project Euler Problem 65 Problem 65 continues our exploration of continued fractions, although this time a different property is the focus: the ability to generate rational fractions that converge on better and better approximations to the number e.
- Project Euler Problem 64 I don’t know how I managed to avoid learning about the properties of continued fractions in school; I can only blame the textbook authors for not including the material. Continued fractions are really quite remarkable; have you ever wondered why some rational fractions (e.g. 1/3) take infinitely many decimals to represent (0.3333…), while other fractions (e.g. 1/4) have a finite representation (0.25)? Or why if you represent these fractions in a different base (e.g. hexadecimal) then they may take a different finite or even infinite number of digits to represent?
- Project Euler Problem 63 Problem 63 asks “How many n-digit positive integers exist which are also an nth power?”
- Project Euler Problem 62 Problem 62 asks us to find the smallest cube which, when permuted, can form 4 other cubes.
- Project Euler Problem 61 Problem 61 is yet another digit manipulation problem. This time, we have to find a set of six numbers that overlap in a cyclic fashion, and each number must be from a different one of six sets (triangular through octagonal number sets). The numbers are all 4 digits long and two digits overlap cyclically at each step.
- Project Euler Problem 60 This was challenging! Problem 60 asks us to find the sum of five primes, any pair of which must – when concatenated in any order – form another prime.
- Project Euler Problem 59 Another fun one! Problem 59 reminds me of those long-past days when I was a young boy, heavily armed with water pistols and secure in my friend’s tree house, trying to develop secret alphabets and substitutions ciphers to keep our secret documents out of the hands of our evil sisters, who generally had no interest in what we were writing anyway.
- Project Euler Problem 58 I figuratively stubbed my toe on problem 58, engineering a rather complex solution when a simple loop would have sufficed.
- Project Euler Problem 57 Project Euler Problem 57 was a little too easy, not even taking 15 minutes to write and test. Even then, I spent the majority of my time staring at the recursive form of the expansion of sqrt(2) until I saw how to write it as an infinite sequence. (A pen and paper may help you figure it out.)(def sqrt2-approx (iterate #(/ (+ (numerator %) (* 2 (denominator %))) (+ (numerator %) (denominator %))) (/ 3 2)))
- Project Euler Problem 56 This was definitely too easy. Problem 56 once again demonstrates how simple it is to play with bignums and strings.(use '[clojure.contrib.math :only (expt)])
- Project Euler Problem 55 For problem 55, we need to count the number of Lychrel numbers below ten thousand. I almost tagged this as too-easy, but I spent about 20 minutes figuring out why my four line solution wasn’t correct (hint: you shouldn’t check if the Lychrel number itself is palendromic).(defn palindromic? [n] (= (seq (str n)) (reverse (str n))))
- Project Euler Problem 54 Poker! In order to solve problem 54, we need to basically model a poker hand and compute the strength of it relative to another hand.
- Project Euler Problem 53 Problem 53 asks us a very basic fact about the number of combinations that can be generated when starting with n objects and removing r of them.
- Project Euler Problem 52 Problem 52 was too easy, so I took the time to use it’s simplicity and study how lazy sequences are chunked, and how they are grouped when apply‘d.
- Project Euler Problem 51 Problem 51 asks us to find a tricky class of prime numbers generated by replacing certain digits of a pattern with the same digit.
- Project Euler Problem 50 Finally, we made it to the 50th problem! In fact, if this were an old-school Japanese RPG, I’m pretty sure we would be hearing some victory music playing about now…
- Project Euler Problem 49 This problem was tricky. Although we get to reuse a significant amount of code for prime?, as-int, and choose-k, we still need to write two rather tricky functions to extract the special triples.
- Project Euler Problem 48 Another one that is too easy in clojure. Problem 48 wants us to find the sum of 1^1 + 2^2 + … + 1000^1000. With Clojure’s built-in bignum support, this is a cinch:(use '[clojure.contrib.math :only (expt)])
- Project Euler Problem 47 Problem 47 is a rather strange computation, because the author of the problem wanted us to bundle together multiples of a prime factor, which I found a little unusual because it means considering a prime number to an exponent as “prime”, which isn’t strictly true. Unfortunately, this additional constraint on the problem meant that rather directly use prime-factors-of from problem 12, the prime factors needed little ‘tweak’ to use the largest multiplicity possible for each prime.
- Project Euler Problem 46 Problem 46 asks us to find the smallest composite number that can’t be written as a prime number plus twice a square.
- Project Euler Problem 45 With the tricks we learned in the last problem, solving problem 45 was a snap.(def triangle-nums (map #(bit-shift-right (* % (dec %)) 1) (iterate inc 2)))
- Project Euler Problem 44 Problem 44 asks us to find the smallest distance between two pentagonal numbers that produce another pentagonal number when added to or subtracted from each other.
- Project Euler Problem 43 More pandigital problem madness for problem 43. Honestly, I think the guys at Project Euler were running out of ideas or something.
- Project Euler Problem 42 For our 42nd problem in Project Euler, we need to find how many words have wordscores that are also triangle numbers. Triangle numbers are generated by the equation 1/2 * n * (n-1).
- Project Euler Problem 41 Problem 41 is yet another variation on the theme of pandigitality and primality. If nothing else, it is teaching me how to reuse my own code…;; from euler-32(defn all-unique? [digits] (let [unique (distinct digits)] (= (count unique) (count digits))))
- Project Euler Problem 40 This one was too easy to brute force.(defn euler-40 [] (let [d (apply concat (map str (iterate inc 0)))] (reduce * (map #(Character/getNumericValue (nth d %)) [1 10 100 1000 10000 100000 1000000]))))
- Project Euler Problem 39 I found this one to be rather interesting, but maybe I just had a lot of coffee this morning and am in an especially good mood. Problem 39 asks us to find the number n < 1000 for which there are the most number of right triangles with integer sides and a perimeter of n.
- Project Euler Problem 38 Problem 38 is essentially just a variation on old themes: find a particular concatenated number that is pandigital when multiplied by the numbers 1, 2, …n. You may note the similarity of the code to problem 32. Without going into detail, here is the solution:
- Project Euler Problem 37 One thing I learned during the course of completing problem 37 is that I have been using the wrong definition of prime? in previous problems. Technically, the number 1 is not in fact prime, yet the old definition of prime? would treat it as if it were.
- Project Euler Problem 36 For problem 36, we need to find numbers that are palendromic in both base 2 and base 10. Thankfully, this is very simple to accomplish if we use the Java libraries to create the binary representations and also reuse a single function we wrote back in problem 4.
- Project Euler Problem 35 For problem 35, we need to compute how many circular primes there are below 1,000,000. Circular primes are numbers for which all rotations of a number are also primes, like (197->971->719).
- Project Euler Problem 34 Ahh, finally a chance to use something I learned shortly after learning it! Problem 34 felt really similar to Problem #30, and the solution even looks similar.(defn factorial [n] (reduce * (range 2 (inc n))))
- Project Euler Problem 33 Project Euler Problem 33 asks us to find a particular pattern of fraction which satisfies several characteristics:
- Project Euler Problem 32 Project Euler Problem 32 asks us to once again find numbers that are pandigital from 1 to 9. This time, the digits of the numbers are taken from the equation (a*b=c), ignoring the * and = symbols.;; Only two possible patterns of multiplications that produce 9 digits;; 1. A 1 digit number times a 4 digit number can be 4 digits long.;; 2. A 2 digit number times a 3 digit number can be 4 digits long. (defn as-digits [num] (map #(Character/getNumericValue %) (str num)))
- Project Euler Problem 31 Project Euler Problem 31 asks us to find the number of possible English coin combinations that add up to £2.
- Project Euler Problem 30 Problem 30 was another very short problem. We just need to find the sum of all numbers that are equal to the sum of the fifth powers of their digits. The only real hard part is to decide at what point we should stop searching. I just arbitrarily picked 1,000,000, and wrote the following.(use '[clojure.contrib.math :only (expt)])
- Project Euler Problem 29 Problem 29 was trivial. It asks us for the number of distinct values generated by the expression a^b, where a and b are between 2 and 100, inclusive.
- Project Euler Problem 28 Problem 28 asks us to find the sums of the diagonals in a square matrix of numbers created by spiraling outward from the number 1 in a clockwise direction.
- Project Euler Problem 27 Project Euler Problem 27 asks us to find the coefficients of a formula that will produce as many prime numbers as possible for consecutive integer values that are inputs.
- Project Euler Problem 26 Project Euler Problem 26 asks us to find number d where 1/d gives the longest recurring cycle of digits. Obviously, since some numbers (such as 1/3) repeat forever when written in decimal form, a lazy solution that takes digits one by one is a good idea here.
- Project Euler Problem 25 Problem 25 asks us to find the index of the first Fibonacci number to have more than 1000 digits. Here’s my first solution, which boils down to making a single, human-readable line at the end.(def fibonacci (map first (iterate (fn [[a b]] (vector b (+ a b))) [1 1])))
- Project Euler Problem 24 Project Euler Problem 24 asks us to find the millionth lexicographic permutation of the numbers 1 through 9. As near as I can tell, “lexicographic” means “in dictionary order”, or simply “sorted”.
- Project Euler Problem 23 Trying to solve this problem the naive way quickly led me into computational problems…(defn proper-divisors [n] "Returns a list of the proper divisors of n." (filter #(zero? (mod n %)) (range 1 (+ 1 (/ n 2)))))
- Project Euler Problem 22 Project Euler Problem 22 gives us our first opportunity to use regular expressions. It’s amazing how a single re-seq basically takes care of extracting data from the file format.
- Project Euler Problem 21 Project Euler Problem 21 asked us to find the sum of all pairs of amicable numbers under 10000. My initial solution was relatively straightforward:
- Project Euler Problem 20 Problem 20 turned out to be yet another ridiculously simple problem for Clojure. Here’s how to sum the digits in 100 factorial:(defn factorial [n] (reduce * (range 2 (inc n))))(defn sum-digits [s] (reduce + (map #(Integer/parseInt (str %)) s)))(defn euler-20 [] (sum-digits (str (factorial 100))))
- Project Euler Problem 19 Although using Conway’s Doomsday Algorithm is a fun party trick, I tend to hate calendar math. Worse, I hate Mondays too. So I guess this problem wasn’t written for me.
- Project Euler Problem 18 Project Euler Problem 18 looked harder than it was. At first, I thought some sort of sophisticated heuristic approach would be needed to keep track of the lowest-cost paths as it incrementally searched through the tree, using some basic graph theory.
- Project Euler Problem 17 For Project Euler Problem 17, I fell back to a more C-style pattern (almost like a big case statement). This is admittedly not the most beautiful solution, but I am comfortable with that as the problem itself doesn’t hide any particular mathematical elegance.(defn tens [n s sub] (if (zero? (mod n 10)) s (apply str (concat s "-"(verbally (- n sub))))))
- Project Euler Problem 16 This problem doesn’t even deserve an explanation and could easily be made a one-liner. Really, computing 2^1000 is just too easy.(defn euler-16 [] (let [s (str (reduce * (repeat 1000 2))) v (map #(Integer/parseInt (str %)) s)] (reduce + v)))
- Project Euler Problem 15 I remembered the answer to this this one from school…probably because my statistics professor was extremely attractive and somehow her words lodged themselves especially deeply in my young mind.
- Project Euler Problem 14 This problem was rather fun to solve. The Collatz sequence is a rather simple pattern that is as-yet mathematically unproven to converge, at least according to wikipedia.
- Project Euler Problem 13 Problem 13 was ridiculously easy. Once again I forgo any numerical trickery, preferring to convert back and forth between strings and large numbers in a casual and easy-to-understand manner:(defn euler-13 [nums] (apply str (take 10 (str (reduce + nums)))))
- Project Euler Problem 12 Project Euler problem 12 was the hardest so far, despite it’s simplicity. I started of course with a brute force approach, since it is quick to write:
- Project Euler Problem 11 Looking back, I think I misinterpreted this problem but accidentally get the right answer anyway.
- Project Euler Problem 10 All that work we did back in problem 7 really paid off for this problem. If we use the lazy prime generating functions we defined earlier, problem 10 has become a one-liner.
- Project Euler Problem 9 Brute force! Side effects! Square roots!? What have I done?! Functional Puritans out there, you may want to shield your children’s eyes!
- Project Euler Problem 8 The definition of Problem 8 suggests some flexibility on how you treat the 1000-digit number: as a number or as a string. I decided that it would be easier to understand as the latter – using mod to extract digits seemed a little redundant and not really the point of the problem, which treats each digit as a distinct object. Why make things more complex than they need to be?
- Project Euler Problem 7 The seventh euler problem requires us to compute the 10001st prime number. To make this problem a bit harder, I decided that the function which will generate prime numbers must be lazy, or at least appear so to the consumer.
- Project Euler Problem 6 Not much to say about this problem. Everyone’s solution seemed similar to my own, with some minor stylistic variation.(def natural-numbers (iterate inc 1))
- Project Euler Problem 5 Here’s the link to the problem description. My first try at the problem resulted in a slow but working implementation.(defn multiple-of-all? [n factors] (every? #(zero? (rem n %)) factors))
- Project Euler Problem 4 As usual, we begin with a link to the problem.
- Project Euler Problem 3 First, the obligatory link to the problem description.
- Project Euler Problem 2 For reference, here is the description of Project Euler Problem #2.
- Project Euler Problem 1 As part of my efforts to learn Clojure, I am starting to work through the Project Euler a little bit each day to sharpen my programming skills without the pressure of having to get any real work done. I’ll post my notes here as I go along for everyone to enjoy, critique, or just laugh at.




